Función

La palabra función hace referencia a aquella actividad específica que realiza algo o alguien en un sistema determinado. Por lo general, la función que cumple alguna cosa o persona se relaciona a su vez con un fin u objetivo determinado. Así podemos hablar de diferentes tipos de funciones de acuerdo al fin o sistema del que se trate.

Concepto de función

Considerando que la función es la actividad que realiza un elemento dentro de un sistema, este concepto es variable y multifacético. En este sentido, podemos encontrar el concepto de función en numerosas disciplinas y ciencias. Entre ellas podemos mencionar algunas como: Economía, Estadística, Física, Ingeniería, Matemáticas, Medicina, Psicología, Química, entre otras.

Por supuesto cada una de estas disciplinas cuenta con su propio concepto de este término aunque volcado en su materia de interés. Pero si buscamos ejemplos de este concepto en la vida cotidiana podemos referirnos a la función como lo que hace algo. Por ejemplo, la función de una silla tiene que ver con la acción de sentarse así como una heladora conserva los alimentos refrigerados.

Concepto de función matemática

En matemáticas se le llama función a la relación que existe entre dos magnitudes. En esta relación ocurre que el valor de la primera magnitud, a la que también se denomina dominio, le corresponde un valor único de la segunda magnitud, también conocida como imagen.

El ejemplo más común de una función numérica se da en la relación entre posición y tiempo en el movimiento de un cuerpo. Aquí podemos mencionar tranquilamente como ejemplo de función la distancia que recorre un vehículo en un tiempo determinado. En esta clase de función se contempla la velocidad y el tiempo para determinar la distancia.

Cuando se representa una función en formato de ecuación se usa la letra f para referirse a la función y f(x) a la imagen. El símbolo x viene a representar en este caso la variable independiente de la fórmula. De esta manera, la variable independiente se fija con anterioridad mientras que la variable dependiente se deduce a partir de la independiente.

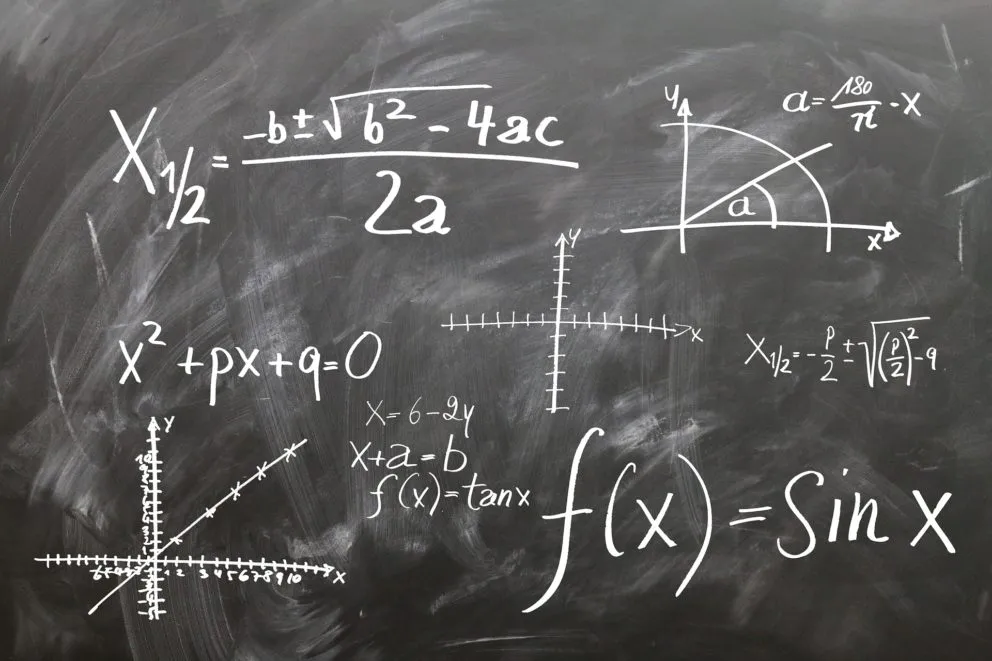
En definitiva, el concepto de función es una regla de correspondencia dada entre dos conjuntos. Así, la correspondencia se presenta cuando a cada elemento de un conjunto le corresponde un solo elemento del otro conjunto. El primer conjunto se conoce como dominio, mientras que el segundo se denomina contradominio o imagen.

Elementos de una función matemática

En toda función existen una serie de elementos específicos que es necesario aprender a identificar. Los principales elementos de una función son los posibles valores que pueden tomar las dos variables que la conforman. Estos representan la variable independiente y dependiente en una función y se conocen como:

• El primer elemento es el dominio y consiste en el conjunto de valores que conforman la variable independiente X en la función.
• El otro elemento se conoce como codominio y es el conjunto de valores que toma la variable dependiente Y.
• Luego está la imagen o rango que son los valores finales que toma la variable dependiente Y.

Las funciones no solo se representan a través de cálculos o ecuaciones, también se las puede graficar. En un gráfico sencillo para ilustrar los elementos de una función podemos decir que: el dominio se encuentra de un lado, el codominio del otro y el rango son las correspondencias que pueden establecerse de un grupo al otro.

Y es que el concepto de función como ya hemos mencionado es una regla de correspondencia. Esto quiere decir que a través de una función podemos relacionar unívocamente dos magnitudes. La primera variable es la independiente y la otra es la dependiente, es decir, depende de la otra variable.

¿Cómo se determina una función?

Las funciones matemáticas pueden construirse como un aparato de cálculo. De esta manera, el dominio es la entrada y los cálculos que se realizan con ellos son la función en sí. Entonces, los elementos del contradominio son los resultados de salida de este aparato de cálculo.

Cuando pensamos la función de esta manera resulta incluso más fácil encontrar el dominio del cual se parte. Como sucede con cualquier otro cálculo u operación, los valores del dominio u entrada pueden representarse con una letra. Por lo general se acostumbra a usar la letra x, pero también puede emplearse la s o cualquier otra letra.

Y así como representamos el dominio con una letra específica, el número de salida también cuenta con su propio símbolo. Por lo general se lo representa como f(x) o f(s), o la letra que se usará para el dominio entre paréntesis. Un ejemplo de función sería el siguiente: f(x) = 2x+ 3x – 5. En esta función se señala que cada valor del dominio se relaciona con el doble de ese número más el triple menos cinco.

Generalmente se establece o especifica el dominio de una función cuando se define la misma. Sin embargo, también puede ocurrir que no se especifican los dominios en funciones definidas por una ecuación. Y si no se especifica directamente, generalmente el dominio en una función suele ser el conjunto con más números reales que den un número real de salida.

Formas de representar la función matemática

Si bien existen diferentes maneras de representar una función matemática, cabe mencionar que la función no sufre alteraciones. Es decir, aunque la función se muestre o describa de distintas maneras sigue siendo la misma. Existen 4 formas principales de representar una función: la representación algebraica, la numérica, la verbal y la visual.

Representación algebraica

Para representar una función de forma algebraica se debe explicar la función con una ecuación explícita. De esta manera, esa ecuación explicará la relación existente entre las dos magnitudes de la función. Lo útil de esta representación consiste en que nos permite conocer las propiedades características de esa función.

Representación numérica

Esta forma de representación emplea una tabla de valores donde se detallan las correspondencias y de cada valor x. Por lo general se usan números naturales del lado izquierdo, mientras que del lado derecho se proyectan los valores otorgados a x. Sin embargo, esta forma de representar la función nos permite poner el valor que necesitamos.

Representación verbal

Además de expresar una función con letras y números podemos escribir un texto describiendo una función. De esta manera, la representación verbal detalla de forma descriptiva cómo se compone la función. Se emplea un lenguaje literal para explicar detalladamente la función y que sea fácil de entender y escribir.

Representación visual

Tal como su nombre lo indica, la representación visual consiste en presentar la función con un gráfico de ejes cartesianos. Aunque cabe mencionar que existen diferentes tipos de funciones que se grafican de acuerdo a sus características y propiedades. Pero la representación visual se nutre además de las representaciones antes mencionadas.

Clasificación de las funciones matemáticas

Para clasificar las funciones se considera tanto su naturaleza como su condición. En base a eso podemos mencionar que las funciones pueden ser algebraicas o trascendentes. A su vez, estos tipos pueden subclasificarse en:

Funciones algebraicas

En este tipo de funciones se pueden realizar distintas operaciones con la variable independiente (adición, división, multiplicación, potenciación, radicación y sustracción). A su vez, las funciones algebraicas pueden ser explícitas, cuando se obtienen las imágenes por sustitución, o implícitas cuando es necesario realizar operaciones para obtenerlas.

Dentro de las funciones algebraicas nos encontramos con las funciones polinómicas que son definidas por un polinomio. Y dentro de las polinómicas se encuentran las funciones constantes, las de primer grado que engloba a las funciones afines, lineales y de identidad. Y por último, dentro de las polinómicas se encuentran las funciones cuadráticas.

Otra subclase de las funciones algebraicas son las funciones racionales donde el dominio está formado por números reales. La siguiente subclase es la de funciones radicales que se basan en un criterio dado por la variable x bajo el signo radical.

Y por último están las funciones a trozos que se definen por criterios basados en intervalos y pueden subclasificarse en: funciones de valor absoluto, función parte entera de x, función mantisa y función signo.

Funciones trascendentes

En este tipo de función la variable independiente se presenta como exponente, índice de la raíz o afectada por algún signo. Dentro de las funciones trascendentes podemos encontrar las funciones exponenciales. En estas funciones le corresponden potencias a cada número real.

Luego se encuentran las funciones logarítmicas que realiza la operación inversa a la exponencial. Y por último se encuentran las funciones trigonométricas que se subdividen en: función seno, función coseno, función tangente, función cosecante, función secante y función cotangente.

Otros tipos de funciones

La palabra función puede emplearse para referirse a otras cosas además de la actividad que realiza algo o alguien. De esta manera, podemos llamar función a un espectáculo, la proyección de una película o bien una representación teatral. Incluso se puede llamar función a un acto religioso, a la conmemoración de un hecho histórico o una fiesta comunitaria.

Pero también podemos hablar de función en campos disciplinarios específicos como sucede con la Lingüística. De esta manera, la función lingüística se refiere al propósito, rol o uso que tiene algún elemento en la estructura gramatical de una oración. Así podemos hablar de funciones lingüísticas fónicas, léxicas, morfológicas o sintagmáticas.

Incluso podemos hablar de función lingüística sobre la relación que tienen esos elementos en la estructura gramatical. Por otra parte, la lingüística distingue seis funciones del lenguaje que son: la función apelativa, la emotiva, la fática, la metalingüística, la poética y la referencial.

Otro tipo de función es la función social, el cual es un concepto propio de la Sociología. La función social se refiere al papel que cumple cada individuo dentro del entramado social. En estos casos, la sociedad se entiende como un sistema estructurado compuesto por diferentes elementos interrelacionados entre sí.

Por otra parte, también podemos hablar de función informática para referirnos a una serie de órdenes programadas para completar una tarea. Con esto nos referimos a la forma en que se programa un software para que realice alguna tarea específica. De esta manera, la función es la encargada de señalar los pasos que se deben realizar siguiendo un orden para realizarla.

Entonces, la función informática pertenece a los lenguajes de programación y se trata de un subalgoritmo con una secuencia de órdenes. Las órdenes que conforman esta función cumplen una tarea específica dentro de una aplicación mayor. Es una herramienta muy útil para los desarrolladores que les permite crear un mejor rendimiento del programa que diseñan.

Preguntas frecuentes

Formato para citar
"Función". En: De Significados. Disponible en: https://designificados.com/funcion/ Consultado: 26 de abril de 2024.